B-Tree – A method used by application storage engines for writing, reading and indexing data optimised for reading. One way of writing data is just to append it to existing data. Then you search for it by reading each piece of data, checking if it’s the right one, and reading the next item if it is not. This can, however, take a very long time if your database or file has a million entries. The longer the file, the worse the average search and read time. We need to index the file or database so we can find entries faster.
A binary search tree and a B-Tree both store index or key:values for data items. A binary tree has a starting point or root, with a few layers of nodes. Each layer is laid out from left to right and a node has a key:value that is greater than nodes to the left and smaller than nodes to the right. To find a particular key, you progress down through the layers in the tree util you arrive at the node with the desired value. The deeper the tree and the more nodes, the longer this takes.
A B-Tree fixes this problem. It has a starting point or root with a small number of node layers called leaves and children. We’ve drawn a simplified diagram to show this. Note that there are different definitions of what is a leaf node and what is not. We have kept things simple and may be oversimplifying.
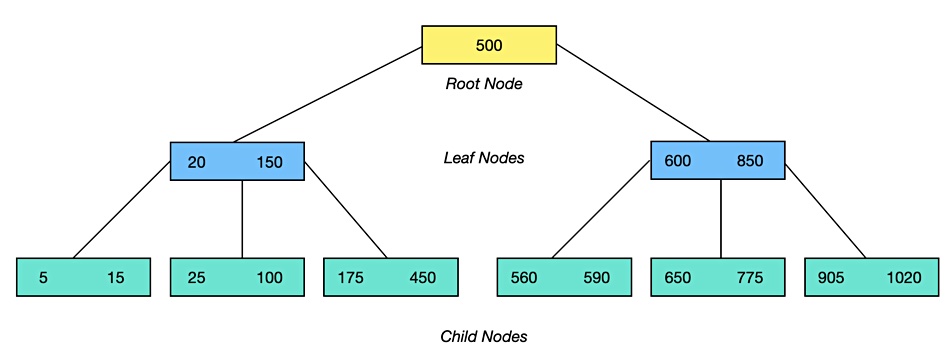
A node can hold one or more keys, up to a limit, which are sorted in ascending order. The numbers in each node in our diagram are range limits. The left-most child node, for example, has a range of keys between 5 and 15. If we have a leaf node with a range of 20 to 150 then we know all key:values below 20 will be in its left-most child, key:values between 20 and 150 will be in the middle child, and keys valued at more than 150, but less than 500, will be in in its rightmost child.
As you add more data, a B-tree gets more index values which have to be added. This can lead to more leaf nodes and child nodes, with nodes being split in two, and reorganization going on in the background.
The B-Tree has far fewer layers than a binary tree which reduces the number of disk access needed to search it. This makes a B-Tree scheme good for read-intensive workloads. A Log-Structured Merge Tree is better for write-intensive workloads.






